HW1 - Problem 2
Problem 2
- Write down the two solutions to \(z^2 = 1\) in the standard notation of complex numbers.
- What are the \(\theta\) if we write the above two solutions in polar notation, that is in the form \(\cos \theta + i \sin \theta = e^{i\theta}\). Draw the two solutions in the complex plane and label the angle \(\theta\) they form with the positive real axis. Verify that for each of the \(\theta\), you get \((e^{i\theta})^2 = 1\).
- What are the three solutions to \(z^3 = 1\) (Hint: It may be easier to find this using polar notation)? Draw them in the complex plane.
- Let the three solutions from the previous problem be 1, \(\omega_3\), \(\omega_3^2\) going in counter clockwise order. Verify that the second solution does indeed square to be the third solution.
- We call solutions to the equation \(z^n = 1\) the \(n\)-th roots of unity. Of particular interest is the first one in the counter clockwise direction after 1, which we call \(\omega_n\). All the other \(n\)-th roots of unity can be constructed once this is known. What is a general form for the value of \(\omega_n\)? As a hint, you will want to use polar coordinates.
- Since complex numbers can be expressed as vectors, we can model addition of complex numbers as vector addition too. Recall that when adding two vectors, you can simply place the first vector at the origin, then the second vector at the end of the first vector. The vector from the origin to the new end point is the sum of the two vectors.
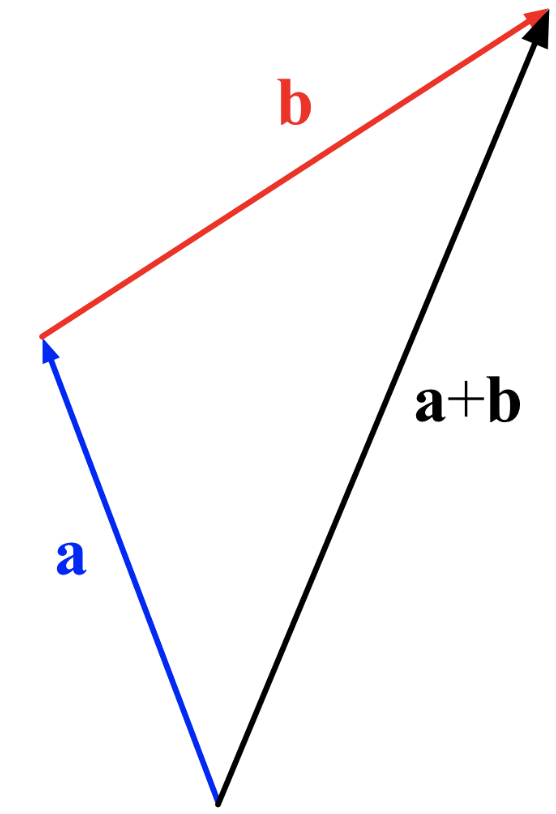
What do you get when you add all three 3rd roots of unity? Briefly justify your solution by drawing the addition. 7. Do you get the same result as above if adding up all the 4-th roots of unity? What if we add all the \(n\)-th roots of unity?