HW4 - Problem 4
Problem 4: Some Computational Complexity
Part A: \(P \subseteq BQP\)
To show that \(P \subseteq BQP\), we must show that quantum computers can simulate classical computation. One problem with simulating classical circuits directly, is that these circuits could be irreversible, which is not possible to directly imitate on a quantum computer. To reconcile this, we need to show that we can simulate classical gates in a reversible way on a quantum computer.
The Toffoli gate takes in three input bits \((a, b, c)\) and negates the third bit \(c\) if and only if \(a \wedge b = 1\).
- Construct a table with the columns INPUT and OUTPUT, where INPUT is all 8 three-bit strings, and OUTPUT shows what the output would be if that bit string was the input to a Toffoli gate.
- Show how to use the Toffoli gate to create a reversible AND gate and a reversible NOT gate.
Part B: Assigning problems to classes
LIQUEENS
LinkedIn has recently added some games, one of which is called Queens. In Queens, you are given an \(n\) by \(n\) grid the is subdivided into \(n\) different connected regions indicated by color. The objective of the game is to place \(n\) queens such that
- there is exactly one queen per color
- there is exactly one queen per row
- there is exactly one queen per column
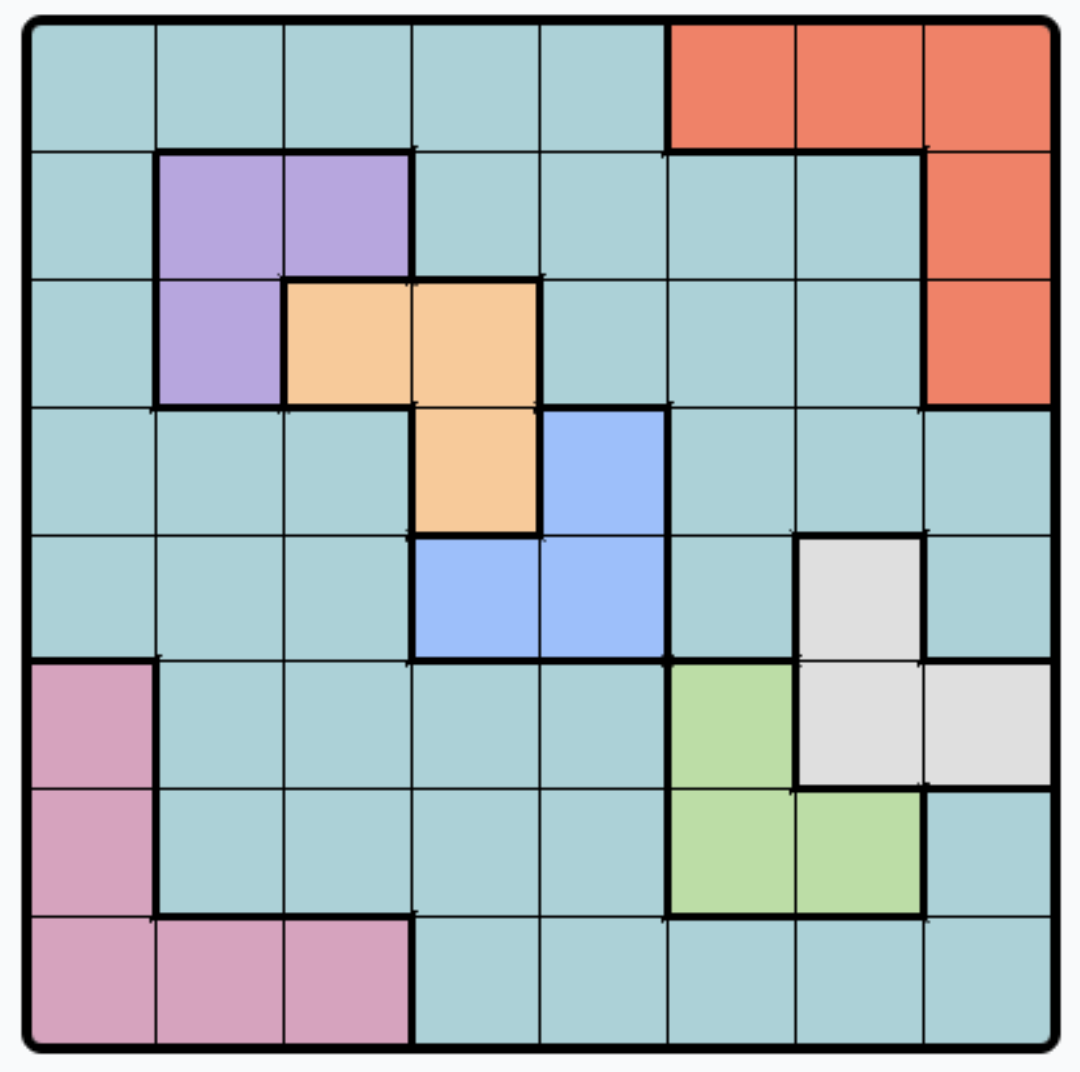
We define the decision problem LIQUEENS to take as input an instance of Queens, and output a 1 if it is solvable, and 0 if it is not solvable.
COLLATZ
- Take any integer \(n\). If it’s odd, multiply it by 3 and add 1. If it’s even, divide it by 2.
- Repeat the above until you reach 1 OR until you get to a number you’ve already seen.
- In the second case, you’ve found a loop, and you will never reach a 1.
The Collatz Conjecture predicts that you can start this game at any positive integer, and you will always get to 1.
We define the decision problem COLLATZ to take as input an integer \(n\) and output a 1 if that \(n\) will get to 1, and output a 0 if that \(n\) will never return to 1.
(EDIT: Feb 11) For the purposes of this problem, you may assume that in the case you can get to 1, this will happen in polynomial time. Of course this is not known, since if we could state this for all n, the open problem would be solved!
Problems
- Solve the instance of QUEENS given in the diagram.
- Is QUEENS in NP? Is QUEENS in co-NP? If you said yes to either, briefly explain why.
- Is COLLATZ in NP? Is COLLATZ in co-NP? If you said yes to either, briefly explain why.