HW6 - Problem 5
Bonus Problem: QFT Counter
(I’ll upload a solution/work through of this problem during week 9. It is a great exercise for getting comfortable with the QFT.)
Suppose \(x \in \{0, \ldots, 15\}\) is a four bit string. Let \(x_1 x_2 x_3 x_4\) be the binary representation of the integer \(x\).
- Express the state resulting from applying \(QFT_N\) to the state \(\left|x\right>\).
- Now suppose that \(y \in \{0, \ldots, N - 1\}\). Let \(y_1\ldots y_n\) be the binary representation of the integer \(y\). Express the output of the circuit below as a function of \(y\) and the \(N\)-th root of unity \(\omega\). Here, we are using the gate
\(P_a = \begin{bmatrix} 1 & 0 \\ 0 & e^{2\pi i/2^a}\end{bmatrix}.\)
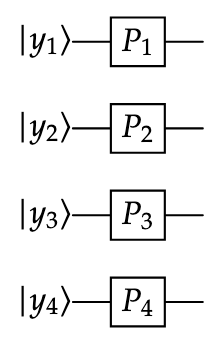
- Put your answer from the first two parts of this problem to express the output of the the following circuit as a function of \(x\).
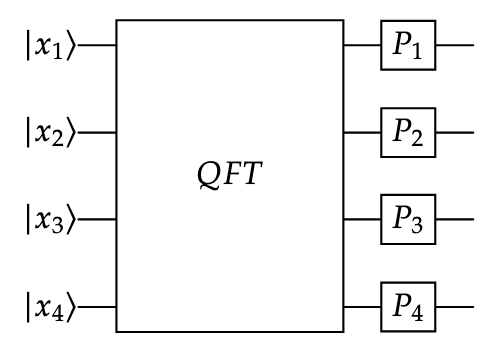
- Finally, express the output of the following circuit. The inverse of the QFT maps from the Fourier amplitudes to the standard basis amplitudes.
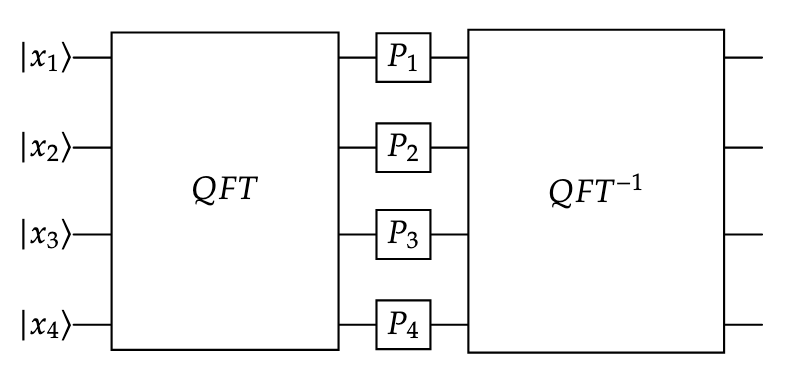
- What was the effect of applying this circuit?